A. Perbandingan Trigonometri
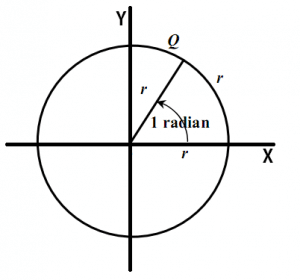
Perhatikan lingkaran dengan pusat O (0, 0) dan jari-jari (r), sedangkan titik A (x, y) pada lingkaran dan sudut dibentuk oleh OA terhadap sumbu X. Pada berlaku r2 = x2 + y2 sehingga diperoleh perbandingan trigonometri sebagai berikut.

1. Rumus Jumlah dan Selisih dua Sudut
a. Rumus untuk Cosinus jumlah selisih dua sudut
cos (A + B) = cos A cos B – sin A sin B cos
(A – B) = cos A cos B + sin A sin B
b. Rumus untuk Sinus Jumlah dan Selisih Dua Sudut
sin (A + B) = sin A cos B + cos A sin B sin
(A – B) = sin A cos B – cos A sin B
(A – B) = sin A cos B – cos A sin B
c. Rumus untuk Tangen Jumlah dan Selisih Dua Sudut
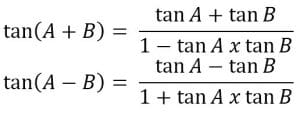
Contoh Soal
Jika tan 5°= p tentukan tan 50°
Jawab :
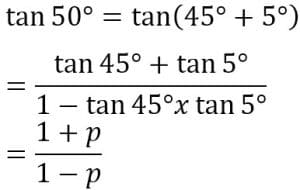
2. Rumus Trigonometri untuk sudut rangkap
a. Dengan menggunakan rumus sin (A+ B) untuk A = B, maka diperoleh:
sin 2A = sin (A + B)
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi,sin2A =2 sin A cos A
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi,sin2A =2 sin A cos A
b. Dengan menggunakan rumus cos (A + B) untuk A = B, maka diperoleh:
cos 2A = cos (A + A)
= cos A cos A-sin A sin
A = cos2A-sin2A ……………(1)
= cos A cos A-sin A sin
A = cos2A-sin2A ……………(1)
Atau
Cos 2A = cos2A-sin2A
= cos2 A- (1 – cos2 A)
= cos2 A – 1 + cos2 A
= 2 cos2 A – 1 ……….(2)
= cos2 A- (1 – cos2 A)
= cos2 A – 1 + cos2 A
= 2 cos2 A – 1 ……….(2)
Atau
Cos 2A = cos2A-sin2A
= (1 -sin2A)-sin2A
= 1 – 2 sin2A ………. (3)
= (1 -sin2A)-sin2A
= 1 – 2 sin2A ………. (3)
Dari persamaan (1) (2) (3) didapatkan rumus sebagai berikut.
Cos 2A = cos2 A – sin2 A
= 2 cos2 A-1
= 1 – 2 sin2 A
= 2 cos2 A-1
= 1 – 2 sin2 A
c. Dengan menggunakan rumus tan (A+B) untuk A=B, diperoleh
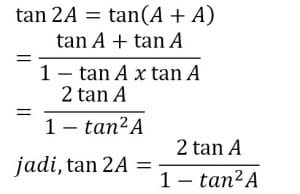
B. Perkalian, Penjumlahan, dan Pengurangan Sinus dan Kosinus
a. Rumus Perkalian Sinus dan Kosinus
- 2 sin A sin B = cos (A- B) – cos (A+ B)
- 2 sin A cos B = sin (A + B) + sin (A-B)
- 2 cos A sin B = sin (A + B)-sin (A-B)
- 2 cos A cos B = cos (A + B) + cos (A- B)
Contoh Soal
Tentukan nilai dari: 2 cos 75° cos 15°
Jawab:
2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
= cos 90° + cos 60°
= 0 + ½
= ½
b.Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus
- sin A + sin B = 2sin ½ (A+B) cos ½ (A-B)
- sin A – sin B = 2cos ½ (A+B) sin ½ (A-B)
- cos A + cos B = 2cos ½ (A+B) cos ½ (A-B)
- cos A – cos B = -2sin ½ (A+B) cos ½ (A-B)
- tan A + tan B =
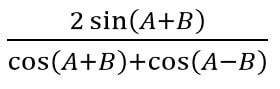
- tan A – tan B =
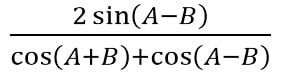
Contoh Soal
Tentukan nilai dari sin 105° + sin 15°
jawab:
sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
C. Identitas Trigonometri
Rumus rumus dasar identitas trigonometri sebagai berikut.
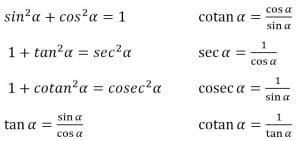
Untuk membuktikan suatu persamaan mempakan identitas atau bukan maka persamaan itu diubah dengan salah satu dari cara-cara berikut.
- Mengubah bentuk ruas kiri sehingga menjadi bentuk ruas kanan.
- Mengubah bentuk ruas kanan, sehingga menjadi bentuk ruas kiri.
- Mengubah bentuk ruas kiri maupun ruas kanan sehingga menjadi bentuk yang sama.
Contoh Soal
Buktikan bahwa sin4 α – sin2 α = cos4 α – cos2 α
Jawab.
sin4 α – sin2 α = (sin2 α)2 – sin2 α
= (1 cos2 α) 2 – (1 cos2 α)
= 1 – 2 cos2 α + cos4 α – 1 + cos2 α
= cos4 α – cos2 α
= (1 cos2 α) 2 – (1 cos2 α)
= 1 – 2 cos2 α + cos4 α – 1 + cos2 α
= cos4 α – cos2 α




Tidak ada komentar:
Posting Komentar